


Next: Conclusions
Up: Liquids. Density Correlation Functions
Previous: Distribution Functions
Suppose energy is the sum of two terms:
U=U0+U1
and we know how to calculate
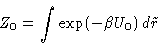
How can we calculate partition function Z?
Idea:

But this is exactly
| 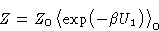 |
(25) |
with 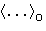 --averaging over reference system with
energy U0:
--averaging over reference system with
energy U0:
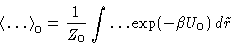
For the free energy:
| 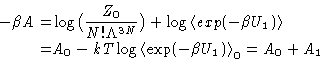 |
(26) |
A1 can be expanded in 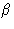 , by expanding
, by expanding 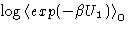 .
.
| 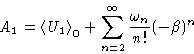 |
(27) |
This makes a series in powers of the perturbation energy U1,
averaged over the
configurations of the unperturbed system.
(They are contained in the 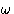 's).
's).
- Van der Waals Equation of state:
- Let's consider the hard-sphere system as a reference, and the
attractive part of the molecular interaction v(r) as a perturbation.
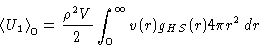
Assuming at low densities:
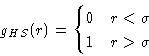

For the hard spheres system:
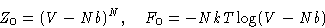
Substituting this into (26,27), and differentiating
with respect to volume, obtain the Van der Waals equation of state:
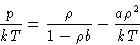



Next: Conclusions
Up: Liquids. Density Correlation Functions
Previous: Distribution Functions
© 1997
Boris Veytsman
and Michael Kotelyanskii
Thu Sep 25 23:59:09 EDT 1997
![]()
![]()
![]()
![]()

![]()
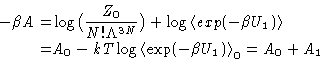
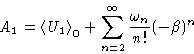
![]()
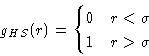
![]()
![]()
![]()