Next: General Case: How to Up: Ensembles and Thermodynamic Potentials Previous: Entropy, Energy and Free
![]()
![]()
![]()
Next: General Case: How to
Up: Ensembles and Thermodynamic Potentials
Previous: Entropy, Energy and Free
We have both energy E and the number of particles N
vary!
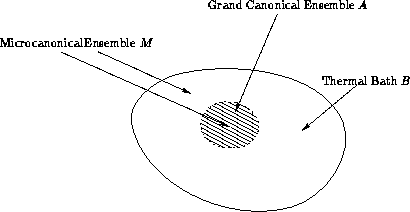
The same considerations as for canonical ensemble (substitute N for
E).
Probability of a state:
![]()
Here
![]()
![]()
Another formula:
![]()
![]()
![]()
Averages:
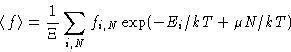
![]() -potential (compare to free energy A!)
-potential (compare to free energy A!)
![]()
Average entropy:
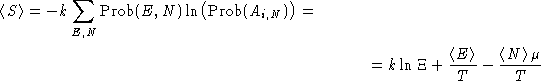
Or:
![]()
| |
(1) |
![]()
![]()
![]()
![]()
![]()