


Next: Landau Theory
Up: Spatial Inhomogeneity. Interfaces
Previous: Problem
Subsections
In the previous
lecture
we obtained for Ising lattice:
| 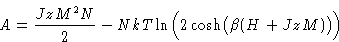 |
(1) |
This is for homogeneous systems. Now M depends on x. We
introduce layers normal to x axis:
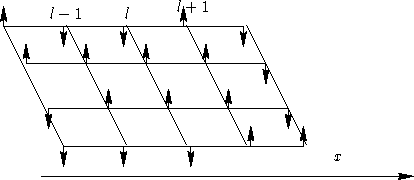
and M becomes M(l).
Consider a simple cubic lattice. Each spin in the layer l has z=6
neighbors:
- One neighbor in the layer l+1
- One neighbor in the layer l-1
- z-2 neighbors in the layer l
Changes to equation (1): substitute N by sum over
layers. Then:
- 1.
- The first term describes mean interaction of a given spin with
z neighbors. Substitute zM2 for
![\begin{displaymath}
M(l)\bigl[M(l+1)+M(l-1)+(z-2)M(l)\bigr]
\end{displaymath}](img9.gif)
- 2.
- The second term describes molecular field acting on a given spin
(in the layer l). Substitute zM by
![\begin{displaymath}
\bigl[M(l+1)+M(l-1)+(z-2)M(l)\bigr]
\end{displaymath}](img10.gif)
- Assumption:
- Magnetization M(l) changes at distances much
larger than the lattice size a0
This means that the difference between neighboring layers is small:
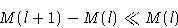
We substitute M(l) by a smooth function M(x) and use the expansion
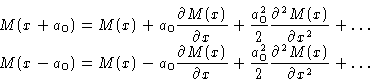
and
![\begin{displaymath}
\begin{split}
\bigl[M(x+a_0)+M(x-a_0)+(z-2)M(x)\bigr] &= \\ zM(x) +
a_0^2\frac{\partial^2 M(x)}{\partial x^2}
\end{split}\end{displaymath}](img13.gif)
We see that in SCF A can be represented as
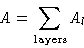
with
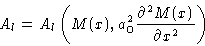
We will not solve the resulting non-linear equations, but
rather use this in the Landau theory.



Next: Landau Theory
Up: Spatial Inhomogeneity. Interfaces
Previous: Problem
© 1997
Boris Veytsman
and Michael Kotelyanskii
Thu Oct 16 20:58:44 EDT 1997
![]()
![]()
![]()

![]()
![]()
![]()
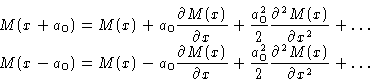
![\begin{displaymath}
\begin{split}
\bigl[M(x+a_0)+M(x-a_0)+(z-2)M(x)\bigr] &= \\ zM(x) +
a_0^2\frac{\partial^2 M(x)}{\partial x^2}
\end{split}\end{displaymath}](img13.gif)
![]()
![]()